Uitslagbepaling en toetsing 'haalbaarheid in één trek'

Bij het dieptrekken van een product moeten we vooraf de uitslag bepalen, deze is globaal te berekenen en zal doorgaans na een proeftrek aangepast dienen te worden. Een te grote uitslag veroorzaakt namelijk ook grotere vervormingskrachten, waardoor de kans op scheurvorming in de gevormde productwand toeneemt.

Uitslag cilindrisch product:

Bij een cilindrisch product kunnen we de uitslag van de blenk berekenen met de volgende

_______

formule: D = √d² + 4dh (hierbij is de productradius op nul gesteld)

Hierin is:

D = diameter blenk

d = diameter product; in feite moet met de neutrale lijn worden gewerkt. Dit is echter alleen zinvol voor producten met een kleine diameter/dikte verhouding

h = hoogte product

Deze aanname leidt tot een grotere blenkdiameter, naarmate de bodemradius groter is. Bij producten met een bolle bodem, is deze aanname niet meer verantwoord.

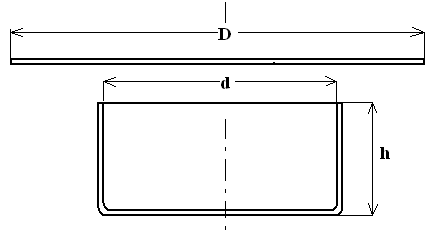
Figuur 7. Platinediameter en product

Uitslag rechthoekig product:

Bij een rechthoekig product hebben we te maken met buigzones op de rechte zijden en dieptrekzones bij de hoeken. Dit betekent dat op deze scheidingslijnen de materiaalspanningen zeer verschillend zullen zijn.

Omdat we de vier hoeken als een hele cirkel kunnen zien met een diameter van 40 mm, zijn de 4 hoeken samen gelijk aan π x d. De rest van de uitslag is hierna eenvoudig te berekenen.

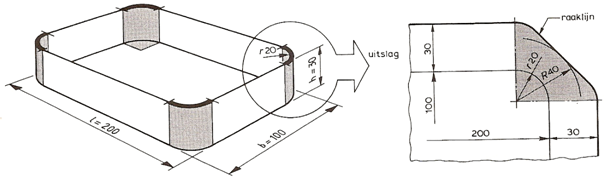
Figuur 8. Rechthoekig product

Voorbeeld radius uitslag bepalen: R = √ r² + 2.r.h = √ 20² + 2.20.30 = √ 1600 = 40 mm

Hierbij:- r = hoekradius van het product

- h = hoogte van het product

Stappenplan rechthoekige producten te vervaardigen in één trek:

Stap 1: teken grondvlak met buigzones: hoogte buigzone = hoogte product

Stap 2: bepaal de radius uitslag: R = √ r² + 2.r.h

Stap 3: bepaal de blenkvorm en controleer of a > R , hierbij a = ( r + h ) . 0,5√ 2)

Stap 4: controleer βo* = a/r < 5 (Bepaal βo = √ A blenk / A stempel)

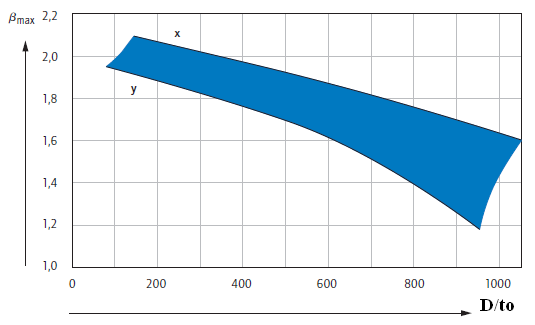
Stap 5: lees βo max. af in de grafiek in relatie met “D”/ to. (“D’= √ 4 / π. Ao)

Stap 6: controleer of βo < βo max.

Uitslag rechthoekig product met flens:

We nemen hierbij het voorbeeld van de vorige pagina als uitgangspositie met daarbij aan de bovenzijde rondom een flens van 10 mm.

Voorbeeld radius uitslag bepalen:

De hoogte h = h + hfl = 30 + 10 = 40 mm

De radius R = √ rfl² + 2.r.h = √ 30² + 2.20.40 = √ 2500 = 50 mm

Voorbeeld 1

We gaan een cilindrisch product met een diameter van 100 mm en een hoogte van 40 mm maken uit een plaat van 1 mm dikte.

Uitwerking:

_______ ______________

D = √d² + 4dh = √100² + 4 x 100 x 40 = 161,2 mm. (We nemen eenblenk van 165 mm)

De totale dieptrekverhouding is: βtot = 165/100 = 1,65

Volgens onderstaande tabel is βo max. ongeveer 2,0. (gem. van x en y)

Dit is groter dan 1,65 en dus kan dit product in één trek gemaakt worden.

Voorbeeld 2

We gaan een vierkant product maken van 50 x 50 mm, met een wanddikte van 1 mm en een producthoogte van 25 mm. De hoekradius is 5 mm. Productmateriaal is DC04 (dieptrekkwaliteit)

Uitwerking:

Stap 1: teken grondvlak met buigzones: hoogte buigzone = h product

Als eerste tekenen we het grondvlak met zijden van 100 mm en afgeknipte hoeken van 30 x 30 mm

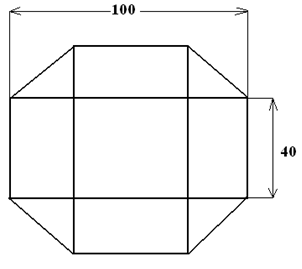
Figuur 9. Uitslag vierkant product

De oppervlakte van de uitslag is dus, 100 x 100 – (2 x 30 x 30) = 8200 mm²

Stap 2: bepaal de radius uitslag: R = √ r² + 2.r.h = √ 5² + 2.5.25 = 16,6 mm

Stap 3: bepaal de blenkvorm en controleer of a > R , hierbij a = ( r + h ) . 0,5√ 2)

a = ( 5 + 25 ) . 0,5√ 2) = 15√ 2 = 21 mm, we voldoen aan de voorwaarde a > R

Stap 4: controleer βo* = a/r < 5 βo* = 21/5 = 4,2 < 5

A blenk = 100 x 100 – 2 x 30 x 30 = 8200 mm²

A stempel = l x b = 50 x 50 = 2500 mm² (radius hoek verwaarloost)

Bepaal βo = √ A blenk / A stempel = √ 8200 / 2500) = 1,81

Stap 5: lees βo max. af in de grafiek in relatie met “D”/ to.

D = √ 4 / π x Ablenk = √ 4 / π . 8200 = 102 mm

D / to = 102 / 1 = 102, βo max. = 2,05 (volgens de grafiek)

Stap 6: controleer of βo < βo max.

1,81 < 2,05 (dus in 1 trek mogelijk)